延續昨天的內容，這邊先貼上示意圖讓大家回憶一下 tree 的結構：

（圖片摘自維基百科）

在搜尋的時候，主要有兩種不同的搜尋策略：深度遍歷 DFS(Depth-First Search) 和廣度遍歷 BFS(Breadth-First Search)。前者是一條路走到黑，一定要先把一條路徹底走完，才會進入到下一條。以上面這張圖來說，就會是以 ABDIK -> EJ -> F -> CGL -> MO -> HNP 的順序進行搜尋。而後者剛好相反，會先每條路都看過一部分，然後再往每條路的下一層走去，因此會是 A -> BC -> DEFGH -> IJLMN -> KOP。

在深度遍歷中，又分為前序遍歷(Pre-order traversal)、中序遍歷(In-order traversal)和後序遍歷(Post-order traversal)。前序就是最一開始提到的，從上到下，從根節點到子節點慢慢走下去。中序遍歷則會從某一側的子節點開始，然後走到跟節點，最後再走另一邊的節點，以上面的圖來說就是 KIDB -> JE -> F -> A -> LG -> OM -> C -> PNH，是一個先從下到上，走到頂點後，另外一邊再次從下往上的過程。後序遍歷則是完全從下到上，當兩邊都從下往上走完後，最後才抵達跟節點，因此是 KID -> JE -> F -> B -> L -> OMG -> PNH -> C -> A。

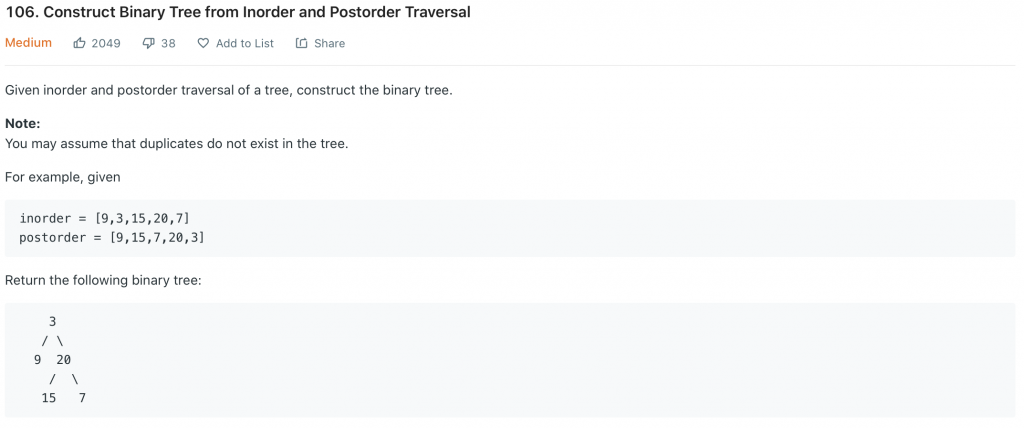
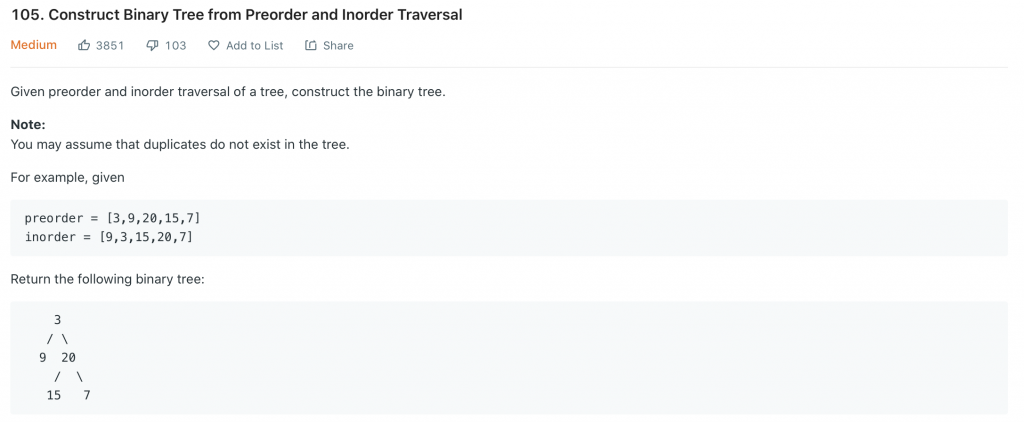
今天的這兩題都是給了兩種遍歷結構，第一題給中序和後序、第二題給前序和中序，然後要重建出整顆樹。解題的方式蠻類似的，以第一題來說，後序遍歷裡面，最後一個數字剛好是根節點，所以我們可以拿這個數字去中序遍歷切，就可以切出前後兩個陣列(以 A、B 代稱)，剛好是左右兩顆子樹。之後再拿後序裡倒數第二個數字，一樣去中序裡面的 B 部份切，就可以切出 B 子樹下方的兩個子樹，這樣一路切下去就建構完成了。

var buildTree = function(inorder, postorder) {    
    let dict = {};
    inorder.forEach((item,index) => {
      dict[item] = index
    })
    
    let recur = function(start, end) {
        if (start > end) return null;
        let val = postorder.pop();
        let root = new TreeNode(val);
        root.right = recur(dict[val] + 1, end);
        root.left = recur(start, dict[val] - 1);
        return root;
    }
    
    return recur(0, inorder.length - 1);  
};

// javascript
var buildTree = function(preorder, inorder) {
  let recur = function(start, end) {
    if (start > end)  return null
    let root = new TreeNode(preorder.shift())
    if (start == end) return root
    let index = inorder.indexOf(root.val)
    root.left = recur(start, index - 1)
    root.right = recur(index + 1, end)
    return root
  }
  
  return recur(0, preorder.length - 1)
};